



Karl Sims
A Fourier transform converts a signal from a space or time domain into
the frequency domain. In the frequency domain the signal is
represented by a weighted sum of sine and cosine waves. A discrete
digital signal with N samples can be represented exactly by a sum of N
waves.
Experiment with the interactive canvas below by adjusting the spatial domain values at the top, or the frequency values on the right. The black curve is generated by the sum of the waves below it. If you adjust the curve samples, the wave amplitudes are updated. If you adjust the wave amplitudes, the curve is updated.
At each frequency, a pair of cos and sin waves are needed to capture
the total amplitude and phase at that frequency. Select the "Amp Phase
Mode" to show the cos and sin amplitudes as 2D controls instead, and a
single wave from the combined cos and sin waves. The control knob's
radius is now the wave amplitude, and its angle is the phase. Try
twirling the knobs around and see how the resulting waves are
affected. For f(0) and f(8), only the cos wave is useful because the
sin is zero at all the sample x locations. Frequency 0 is just the
average of the input values, and shifts the entire curve up and down
when adjusted.
Sums of rotations
One way to compute a frequency domain wave amplitude is to multiply each input sample by each sample of that wave, sum those products, and then normalize by dividing by the number of input samples. This gives the "similarity" of the input signal to that wave, and is the amplitude of that wave's contribution to the input signal. A convenient way to multiply a value, x, by both cos(a) and sin(a) together is to perform a 2D rotation of the vector [x, 0] by the angle a, which gives the vector [x cos(a), x sin(a)] in one step. (This vector can be considered a complex number with real cos and imaginary sin components.) Using this method, f(1) is just the sum of each input x(i) rotated by i/N revolutions. And f(2) is the sum of each x(i) rotated by 2 i/N revolutions, and so on, with normalization as needed. The contribution of any input x(i) towards a given output f(j) is just x(i) rotated by ij/N revolutions. In Amp Phase Mode above, if you hit Zero All and then turn the second input value way up or down, the column of frequency vectors should form a rotation pattern.
Inverse Fourier transform
An inverse Fourier transform converts from the frequency domain back to the space or time domain. Interestingly, this can be performed using nearly the same computations as the forward transform, with the normalization step omitted. For the forward transform we found the weight of each wave, and for the inverse transform we add up waves. Each spatial domain value x(i) is the sum of each scaled cos and sin wave at that sample location. These scaled waves can also be generated by rotating the frequency domain vectors. To find x(i) we can sum each f(j) vector rotated by -ij/N revolutions, although in this case only the cos (real) component of the final sum is relevant since x(i) is scalar.
Audio signal processing
We perceive sound in the frequency domain. The cochlea in our ear actually performs a biological Fourier transform by converting sound waves into neural signals of frequency amplitudes. It can be useful to also process digital audio signals in the frequency domain. For example tuning the lows, mids, and highs of an audio signal could be done by performing a Fourier transform on the time domain samples, scaling the various frequencies as desired, and then converting back to an audio signal with an inverse Fourier transform.
2D image convolution
The frequency domain of 2D data can be found by applying a Fourier transform in one dimension, then processing that result by another Fourier transform in the second dimension. For color images this is done for each RGB channel, and can be useful for blurring, sharpening, compression, or applying arbitrary image convolutions. Multiplying in the frequency domain is equal to convolving in the spatial domain, as stated by the convolution theorem. For large convolution kernels it can be practical to Fourier transform both the image and kernel, multiply, and then inverse Fourier transform to get the convolution result. A wrap-around effect can be prevented by initially padding the image borders with some zeros.




Fast Fourier Transform
A fast Fourier transform, or FFT, is a clever way of computing a discrete Fourier transform in Nlog(N) time instead of N2 time by using the symmetry and repetition of waves to combine samples and reuse partial results. This method can save a huge amount of processing time, especially with real-world signals that can have many thousands or even millions of samples.
Below is a "butterfly" data flow graph for a 16-sample FFT. Each output is the sum of the inputs rotated by various amounts, but the rotations are done in stages after combining subsets of the inputs. Rotations are shown in the graph as R(a) where a is the angle in revolutions, and the rotated results are 2-vectors containing both the cos and sin values together. You can select any of the outputs or inputs to highlight the parts of the graph that set or are set by that value. Small blue arrows will also appear on the side to indicate the input's required rotation for the given output.
Click on the zero frequency output f(0) on the right, and notice that all the inputs are just summed with a binary tree to give that result with no rotations. The normalization step is not shown, but f(0) becomes the average of all inputs when scaled. Click anywhere else on the canvas to clear your selection.
Next select the f(1) output above on the right. The differences from the 1st stage are rotated by 0, 1/16, 2/16, 3/16, etc, to find the cos and sin wave components of frequency 1. Since the second half of the input data was subtracted from the first half, and a negation is the same as a 1/2 rotation, the second half ends up rotated by 8/16, 9/16, 10/16, 11/16, etc as required. These rotated values are then summed with another binary tree to give the f(1) result.
For the f(2) output, each half of the input samples gets an identical cycle of rotation, so the sums from the first stage can be processed recursively in a similar way. The second 4 samples are subtracted from the first 4, then rotated for frequency 2, and also summed.
For the f(3) output, the partial results from stage 1 are further rotated. The rotations for f(1) were 0, 1/16, 2/16, 3/16, etc, but now they need 3 times that, so they are rotated by an additional 0, 2/16, 4/16 and 6/16 to transform from f(1) to f(3). A negation is the same as an 8/16 rotation, and a negation followed by a 2/16 rotation is the same as a 10/16 rotation, etc, so the second 4 are again subtracted from the first 4 before rotating and summing. This pattern continues recursively to combine rotations and generate all the results. The path from any input x(i) to any output f(j) should receive a total rotation equal to ij/16 revolutions, modulo 1.
The FFT output values are not initially in order and are reshuffled in a final stage using their bit-reversed index, referred to as a "twiddle factor". An alternate version of this graph is to shuffle the input order first and apply the FFT process in the other direction starting with nearby samples.
Frequencies above N/2 are typically redundant because the aliasing from sampling at higher frequencies creates results similar to the lower frequency waves. Specifically, f(N-i) equals f(i) with its sin component negated (the complex conjugate) as if rotated in the opposite direction. However, if these higher frequencies are ignored, some lower frequency amplitudes may need to be doubled to compensate before an inverse transform, such as f(1) to f(7) in the first interactive example above.
For an inverse FFT, the frequency vectors can be provided as inputs instead. A helpful alternative to reversing the FFT rotations for the inverse transform is to first negate the sin components of the frequency inputs. This allows the same FFT graph to be used either forwards or backwards for either the forward or inverse transform.
Non-power-of-2 FFTs
When using a "radix-2" FFT as above, input data with non-power-of-2 sizes needs to be enlarged and padded to the nearest power of 2 before processing, but FFT options for other sized steps are also possible. Here is a butterfly graph that shows a radix-3 FFT applied to 9 samples. (This one is not interactive.)
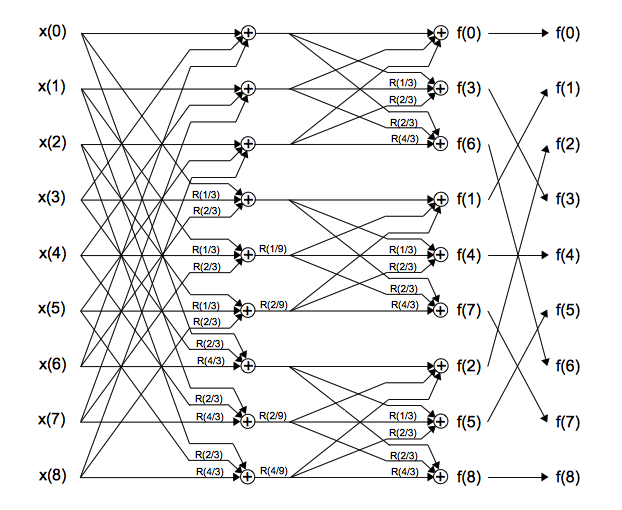
In the special case of radix-2, the (-) nodes performed a 1/2 revolution on the second input as a subtraction, but here R(1/3) and R(2/3) etc are needed on the inputs before combining the 3 segments of the curve in 3 different ways. In this graph, the final stage shuffles by reversing base-3 digits, and the path from any input x(i) to any output f(j) should receive a total rotation of ij/9 revolutions.
Mixing different sized FFT steps can also be useful. For example, radix-2, radix-3 and radix-5 steps could be combined to process any data sizes with factors of 2, 3, and 5, which would provide more size options and often require less padding. Depending on your hardware, larger radix steps may also be more effecient due to fewer total data read/writes, even though they require more calculation.
For more info:
Wikipedia FFT page
Cooley-Tukey algorithm
Convolution theorem
Jez Swanson's Intro to Fourier Transforms
Hearing with the Fourier transform
Back to Karl Sims homepage