Fluid Flow Tutorial

Fluid Flow Tutorial Karl Sims This tutorial illustrates a simple technique for simulating 2D incompressible fluids for visual effects. We'll skip the usual discussion of the classic Navier-Stokes equations, and instead focus on a specific implementation, much of which is derived from Jos Stam's Stable Fluids method.
Flow field A flow field is represented by a grid of velocity vectors. The example on the right shows rotational vortex motions about two centers. Visualization A flow field can be visualized by advecting tracer particles or textures through it. Particles can be "pushed" through a flow field by reading the flow velocities to move their positions, but images are "pulled" by warping them in the local direction of flow. For the examples below, animation cycles were made by repeatedly inserting lines of particles or stamping a checker pattern in the tracer image over time.
Particles are pushed: each particle's position is updated by the flow velocity at the particle's current position, interpolating between flow vectors as appropriate.		Textures are pulled: a tracer image is repeatedly warped by reading color values from upstream pixels in the negative direction of flow. The image is typically at higher resolution than the flow field.
Fluid momentum The visualizations above show tracers moving through a static flow field, but the flow itself can also dynamically change over time. To simulate fluid momentum, the flow field can simply flow itself. Flow vectors are updated by reading interpolated values from upstream grid cells in the same way the tracer image is advected above. New vector values are pulled from the negative direction of flow. Momentum on its own causes circular flows to expand away from their centers which would create lower pressure areas analogous to those occurring at the center of hurricanes or tornadoes. To properly simulate incompressible fluids, we next need to even out the pressure differences caused by diverging and converging flow.		A flow field warps itself by reading from upstream values.

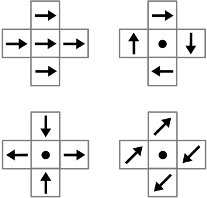
Divergence

Divergence is a measure of the local expansion in a vector field, and is calculated at a given point by summing the outward components of neighboring vectors. Negative divergence corresponds to contraction. Translation, rotation, and shearing motions have zero divergence because their inward and outward components are balanced.

Positive divergence Negative divergence Zero divergence

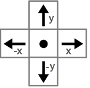
The divergence at the center of a given cell can be found by summing the x component of the vector to its right, minus the x of the vector to its left, plus the y of the vector above, minus the y of the vector below: Similarly a divergence value at the corner between cells can be found by summing the dot products of the adjacent cell vectors with the outward diagonal vectors:

divergence at center divergence at corner

Removing divergence

To enforce incompressibility and remove changes in pressure, we attempt to zero out the divergence throughout the flow field. This is done by adding flow away from high pressure converging areas, and toward low pressure diverging areas. A gradient is the slope or rate of change of a value across a grid. The gradient of the divergence is a vector field that points from high pressure to low pressure areas. So to remove the divergence from a flow field, we repeatedly increment it by the gradient of its divergence.

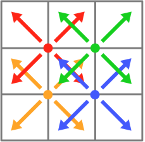
We can combine the divergence and gradient calculations, and if we find divergence values at the corners between grid cells instead of at their centers, we can use a simple 3x3 convolution for this. The left image below represents four local divergences in different colors. Each divergence value is the sum of the outward diagonal vector components of the 4 adjacent cells. The horizontal (x) gradient at the center cell is found by the two right divergence values minus the two left (green + blue - red - orange). The vertical (y) gradient is found by the two top minus the two bottom (red + green - orange - blue).

Divergence at 4 corners Divergence x gradient Divergence y gradient

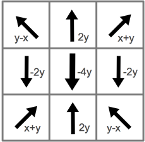The divergence x and y gradients are shown above as 3x3 grids of vectors, and the neighboring flow vectors in those directions (dot products) can be summed for that gradient component of the center cell. For stability, the gradient is scaled by 1/8 before adding it to the flow field. Combining these x and y gradients using vector operations, the kernel code to update each flow-field vector might look something like this:

f'[x,y] = f[x,y] + (dot(f[x-1,y-1] + f[x+1,y+1], {1,1}) +
                    dot(f[x-1,y+1] + f[x+1,y-1], {1,-1}) * {1,-1} +
                    (f[x-1,y] + f[x+1,y] - f[x,y-1] - f[x,y+1]) * {2,-2} +
                    f[x,y] * -4) * 1/8

where f[x,y] is the vector at location x,y of the flow field, f' is the updated flow field, and {i,j} are constant vectors. This step is performed many times to spread the incompressibility across the flow field, perhaps 50 iterations per frame or more depending on the resolution and fluid behavior.

The images below show an initial vector field in red with non-zero divergence, and the results in blue after divergence removal. On the left, the outward momentum forces from a rotation are cancelled giving more stable swirls. On the right, the effect of an external pulse at the center is spread throughout the grid and starts to generate a pair of vortices like a canoe paddle in water.

divergence removal of expanding swirl divergence removal of impulse

Removing divergence from the red vector field prevents swirls from spreading outward. Removing divergence from an external pulse propagates it into a vortex pair.

Boundary conditions

To find divergence values at the cells on the edge of the grid, we need to generate flow vectors from just outside the grid. Different methods for this can give different edge behaviors:

Zero: using a value of zero beyond the grid will avoid flow toward or away from the boundary, as if the fluid is contained in a box, because any edge cell's component of flow normal to the boundary would typically create a non-zero divergence and be removed. The divergence-removal examples above used this mode.
Repeat: repeating the flow value from the nearest edge cell will instead allow flow toward or away from the edges as if the fluid can exit or enter the grid.
Scaled repeat: combining zero and repeat edge-modes can also be useful. Using a scaled value of the nearest edge cell can give a soft boundary effect that slows down the flow at the edges but doesn't completely stop it. Alternatively, using zero for the flow component normal to the boundary, and repeat mode for the component parallel to the boundary, can give a more slippery edge effect.
Wrap: copying the flow value from the opposite side of the grid can create a wrap-around behavior where flow exiting on one side of the grid enters on the other.

Obstacles can also be added to the grid with similar boundary conditions by forcing the flow, or its normal component, to zero at their locations.

External forces

Realistic looking fluid behavior can be generated by alternating between the fluid momentum and divergence-removal steps described above. However some non-zero flow velocity needs to be set somehow, either procedurally or interactively. For example, adding linear flow at specific locations can create a squirting ink effect (see below), or tracking mouse or camera motion can be used to interactively push the fluid.

Other forces can be added to simulate various physical phenomena:

Gravity or buoyency can affect some parts of the fluid differently than others using a tracer image that represents the fluid density.
Damping or friction can reduce the flow velocity over time.
Viscosity can be simulated by diffusing the flow field slightly at each time step so the velocities become more like their neighbors. Note that the repeated resampling of the flow field will also cause a small amount of diffusion.
Cohesive forces can be approximated by using a tracer image to track different fluid substances, such as oil vs water, and then pushing the substances toward areas of the same type, moving convex boundaries inwards and concave boundaries outwards.

Summary of procedure
For each fluid simulation time step:

Advect flow for momentum
Add external forces
Remove divergence (multiple iterations)
Update tracers for visualization
fluid flow simulation of colored ink jets

Multi-grid efficiency

The divergence removal process can be sped up significantly using multiple grid resolutions. We can average the flow field down to half-res and remove the divergence from that, then add the difference between the processed and original half-res grid back to the full-res grid, and finally perform a few divergence-removal iterations at full-res. This can be done recursively so most of the work is done at 1/4 or even lower resolution, which easily allows for real-time results when implemented on a modern GPU.

Accuracy

This method is meant to create useful visual results rather than accurately model physics, but here are a few tips that might reduce unwanted artifacts. For fast moving fluid, use multiple fluid simulation time steps per frame. Use higher resolution for tracer images than for the flow-field grid. Use smooth bicubic interpolation if possible when reading from tracer images and flow fields. For repeated warping of tracer images that aren't being modified in other ways, temporarily warp their coordinates instead, and then resample after multiple iterations.

These methods are extendable to 3D, using volume data for flow fields and tracer images, and 3x3x3 convolutions for divergence removal, but of course it may be more difficult to generate 3D results in real-time, depending on your hardware and volume dimensions.

References

Jos Stam, "Stable Fluids", SIGGRAPH 1999 Conference Proceedings
Navier-Stokes equations

Visit Flow, an interactive exhibit at MIT that employs these techniques.

Back to other work by Karl Sims

The divergence at the center of a given cell can be found by summing the x component of the vector to its right, minus the x of the vector to its left, plus the y of the vector above, minus the y of the vector below:		Similarly a divergence value at the corner between cells can be found by summing the dot products of the adjacent cell vectors with the outward diagonal vectors:

	Divergence at 4 corners		Divergence x gradient		Divergence y gradient


Removing divergence from the red vector field prevents swirls from spreading outward.		Removing divergence from an external pulse propagates it into a vortex pair.