Puzzle Hints and Answers
These are just my solutions: no guarantees they are correct!
I've put blank spaces between answers so you don't see other answers
by accident.

Strange Trip Hint: there are more than 2 places it could be.

Strange TripAnswer:
At the south pole.
Or, 100 miles south of any point on the circle
around the north pole that is 100 miles in circumference.
Or, 100 miles south of any such circle whose circumference is an
integral fraction of 100 miles.

Three Cards Hint: it is not 50% as you might think.

Three Cards
Answer:
2/3. Two of the three blue sides have blue on the other side.
You might think the chances are 1/2 because you could have one of
two cards, but you actually get a side at random, not a card, so you
are more likely to have the blue/blue card than the red/blue card.
Here is another way to think of it: When you pick a card at random,
the chances of it being the same on both sides (either all red or all
blue) are 2 out of 3, and this doesn't change just because you see
one of the sides. If they did, they'd change no matter which color
you saw, and it wouldn't even matter if you looked. So when you do
see the blue side, the red/red card is eliminated, but the blue/blue
card still has a 2/3 probability.

For something else see: CodePix.
Or other links here
or here
or here
or here
or here.
or here.


Monty Hall Problem Hint: it is not 50/50 as you might think.

Monty Hall Problem
Answer:
You should switch. Your chances are 2/3 if you do. Switching always
works if your initial pick was wrong (2/3 of the time) and only fails
if your initial pick was right (1/3 of the time). The initial chances
of your first choice were 1/3, and opening another door without the
prize doesn't actually change that, so the remaining door now has a
2/3 chance because the chances of all possibilities must sum to 1.
Many people think the chances are 1/2 because there are two doors
left, but that is not correct. If you're not convinced 2/3 is
correct, consider a 100 door version: you pick 1 door and Monty opens
98 other doors avoiding the one with the prize. Now you have a 99%
chance if you switch.
Note however that if Monty doesn't always open an empty door, the
chances may be different. For example if he opens a random door, or
if his opening another door is conditional on your initial guess,
then 2/3 is no longer correct. In some versions of this problem
Monty's process is not fully described, which makes a clear correct
answer more difficult.

4 Door Monty Hall Problem Hint:

4 Door Monty Hall Problem
Answer:
Yes, your chances are 5/8 if you switch. The initial chances of your
first choice were 1/4, and opening another door without the prize
doesn't change that, so the remaining 2 doors now have a 3/8 chance
because the chances of all possibilities must sum to 1. But then when
Monty opens door 3, using the same reasoning, door 2 stays at 3/8
chance and so the remaining door changes to 5/8.

Monty Fall Problem Hint: the random way the door is picked does make a difference.

Monty Fall Problem
Answer:
Your chances are 1/2 whether you switch or not. This result differs
from the standard Monty Hall Problem because here Monty might have
opened the door with the prize. We ignore those cases because we are
told he didn't, but it still affects the odds. If your initial pick
is correct, a random other door will always be empty, but otherwise it
is only empty half the time. If you picked door 1, there are 4
equally likely cases where the randomly opened other door is empty:
the prize is in door 1 and door 2 is opened, the prize is in door 1
and door 3 is opened, the prize is in door 2 and door 3 is opened, or
the prize is in door 3 and door 2 is opened. Since 2 of the 4
empty other doors occur when you picked correctly, your chances are
1/2 if you switch or not.

Two Envelopes Hint: the expected value should be the average
of 2 X and 1/2 X which is 1.25 x (?)

Two Envelopes
Answer:
This problem is also known as the exchange paradox, and it is
confusing because it appears that the expected value is the average of
double and half which is 1.25 X so you should always switch. However,
this would be true for any value of X you find, so it wouldn't even
matter if you open the envelope. This same logic suggests that you
should also immediately switch back to the original envelope again,
which doesn't make sense at all.
The fault in this reasoning is that you are not given enough
information to know that double and half are equally probable. You
would need to know more about the probability distribution of possible
amounts, or the process by which the amounts in the envelopes were
determined. For example, if there was a known limit for the amounts,
you would switch only if 2X was within that limit. Note that
it is impossible to have an even distribution of all possible values
without also having an upper bound. If the amounts can go to
infinity, there would have to be some uneven probability distribution,
and you would need to know about that to solve the problem properly.
Given the lack of any information like this, I believe the correct
answer is: It does not matter if you switch.

Three Envelopes Hint: yes there is a way.

Three Envelopes
Answer:
Yes, you can get the best envelope 1/2 of the time. Always open a 2nd
envelope. If it is larger, keep it. If it is smaller, open the 3rd
envelope.
After opening 2 envelopes, the largest of those has a 2/3 chance of
being the best, and the unopened 3rd envelope has a 1/3 chance of
being best. With this strategy, half the time (when the 2nd is
larger) you're improving your odds from 1/3 to 2/3. The other half
(when the 2nd is smaller and you switch to the 3rd) they're still 1/3.
So on the average your chances are 1/2.

What's Next? Hint: what symmetry do they all have?

What's Next?
Answer:

Look at just the right-hand side of each figure.

Helium Hint: air is heavier than helium.

Helium
Answer:
It moves backwards. The deceleration pushes the air in the car
forwards which causes the balloon to move in the other direction.

Urns with Balls Hint: you can do better than 50/50.

Urns with Balls
Answer:
74/99. Put 1 white ball in one urn and the rest in the other.

Bean Bag Hint: it is not 50/50 as you might think.

Bean Bag
Answer:
2/3. You might think it should remain at 1/2 since you didn't
change the initial state of the bag, but this is incorrect. There are
3 equally probable ways you could pick a white bean: 1st bean was
black and 2nd was picked, 1st bean was white and 2nd was picked, or
1st bean was white and also picked. 2 of those 3 have a white bean
left in the bag.

Apples and Oranges Hint:

Apples and Oranges
Answer:
You only need to inspect one piece of fruit. Take it from the "apples
and oranges" box. If it's an apple, that box must be all apples,
since all boxes were labeled wrong. Then the box labeled "oranges"
must actually be apples and oranges because we now know it's not
apples, and finally the box labeled "apples" must be oranges.

4 Boxes of Fruit Hint: you can actually know both how many
guessed 3 and 4 of them correctly.

4 Boxes of Fruit
Answer:
Nobody guesses only 3 correctly, and 7 guess all 4 correctly. If you
get 3 right you'll always get the 4th one right as well.

Four Trees Hint: yes it could be. How?

Four Trees
Answer:
Yes. If one or more trees are on a high hill they could form a
tetrahedron and all be equidistant.

Suicidal Spots Hint: what would happen if
only one had a red spot?

Suicidal Spots
Answer:
They are all dead. Solve recursively: If only one had red he knows it
must be him. After he goes, the others know he must have seen only black
spots, so then they all go. If two have red, they see only one other red,
and when the one other doesn't go the first morning, they both go the
second morning, etc.

One Question Hint:

One Question
Answer:
"Which path would your brother tell me leads to the cannibals?" then
go that way. Or to ask just one person: "If I were to ask you which
path leads to the cannibals, what would you say?" and go the other way.

Three Random Hats Hint: 75% is possible.

Three Random Hats
Answer:
If the 2 hats you see are the same, guess the opposite color,
otherwise pass. If all 3 players use this rule, it works 75% of the
time. It fails only when all the hats are the same color.
This is a little counter-intuitive because your chances of having a
blue hat are still 50% even if you see 2 red hats, so each player will
guess wrong half of the time. However, all 3 players will be wrong
at the same time in 2 of the 8 cases (all red or all blue).
For the other 6 of 8 cases, one will guess right, and the others pass,
so it still works.

Two Random Hats Hint: there is a way that allows them to always succeed.

Two Random Hats
Answer:
One person always guesses the color of the other's hat. The other
person always guesses the opposite color of the other's hat. This
always works! If the hat colors are the same, they guess different
colors and one of them is always right. If the hat colors are
different, they guess the same color and one of them is always right.

String Around the Earth Hint:
does it matter how large the earth is?

String Around the Earth
Answer: a cat
The circumference of a circle is 2π times its radius. If we
increase the circumference by 1 meter, the radius will increase by 1 /
2π times that amount, which is about 16 cm: plenty of room for a cat to
crawl under. Note that the size of the circle doesn't matter.
The circumference and radius, and the change in circumference and
radius, have the same linear relationship for any size circle.
Interestingly, when people answer this puzzle using intuition, rather
than calculation, they almost always guess too low.

Northwest Spiral Hint:

Northwest Spiral
Answer:
√2.
The second pilot is always heading 45° off from north, so he always needs to travel
√2
farther to make the same northerly progress.

Odd Ball Hint:

Odd Ball
Answer:
Yes, first weigh 4 balls vs 4.
If they balance:
You know the odd ball is one of the other 4 and you can divide-by-2
search from there by just weighing 2 of them and then 1 against the
normal balls.
If the initial 4 vs 4 don't balance:
Name those 8 balls H or L for heavier and lighter as appropriate,
and call the other normal balls N.
Balance (H H L L) vs (H L N N).
If that balances:
You know the odd ball is one of the other two H or L, which you can
determine with a final weighing as above.
If that doesn't balance:
You have narrowed it down to 3 possible balls, because the tipping
direction must be consistent with the previous weighing.
If the (H H L L) side is heavier:
It must be one of those 2 H or else the L from the other side.
Weigh those 2 H balls against each other:
If it balances: the L from the other side is the odd ball.
If it tips: the heavier one is the odd ball.
If the (H H L L) is lighter, do the symmetrical thing as above reversing L and H.
There are variations on this scheme that also work.

Six Balls Hint:
You should weigh 2 vs 2 first, but which ones?

Six BallsAnswer:
Yes.
First weigh 1 red + 1 white vs 1 red + 1 blue.
If it balances: each side must have one heavy and one light, because
the reds can not be equal. So the white and blue must each weigh
the opposite of the red they were weighed with. For the second test just
weigh the two reds against each other to determine which of the two
cases you have, and you are done.
If the initial test tips: you know which red is heavy, because it
could never tip towards the light red. The white and blue could be
equal (both heavy or both light) or they could match the reds with one
heavy and one light. (They can't both weigh opposite of the reds or
it would not have tipped.) For the second test, weigh the 2 reds vs
the same white and blue. If it tips, the white and blue are both
heavy or both light depending on which way they tip. If it balances,
the white and blue are different, and you know which is heavier based
on how the first test tipped.
There are many variations on this strategy that also work.

Bags of Gold Hint:

Bags of Gold
Answer:
Take 1 piece from the 1st bag, 2 pieces from the 2nd bag, and so on up to
9 pieces from the 9th bag. The total weight W would normally be 45. If
it is, the 10th bag has the lighter pieces. Otherwise the number of
the guilty bag is (45 - W) x 10.

Fair Cake Hint:

Fair Cake
Answer:
A cuts off a piece. B has the option to reduce that piece and take
it, and then C has the same option. The remainder of the cake is
split between the other 2 people with the usual "one cuts and the
other chooses".
Alternate recursive method: Starting with approximate thirds, each
person can swap with either of the other 2 but then must give at least
a crumb back to whoever he swaps with. This cycles until nobody wants
to swap anymore.

Light Switches Hint:

Light Switches
Answer:
Start with all switches off. Turn switch A on and wait 10 minutes or
so. Turn A off and B on. Go into the room. Light A is off and warm,
B is on, and C is off and cold.

Grid of Tiles Hint:

Grid of Tiles
Answer:
No. If the grid is checkered, each tile must cover 1 black and 1 red
square. However both missing corners are the same color, so there
must be 2 squares with the other color that can never be covered.

1x3 Tiles Hint:

1x3 Tiles
Answer:
Yes. The 1x1 tile can only be in a 3,3 position. If you label the
squares of the grid as follows:
X . , X . , X .
, X . , X . , X
. , X . , X . ,
X . , X . , X .
, X . , X . , X
. , X . , X . .
X . , X . , X .
, X . , X . , X
Each 1x3 tile must cover exactly one of each type. There is one more
X than dots or commas so the 1x1 square must cover some X position. If
you turn this pattern the other way, the same should still be true, and
there are only four X positions that remain X after you turn it:
, X . , X . , X
X . , X . , X .
. , X . , X . .
, X . , X . , X
X . , X . , X .
. , X . , X . .
, X . , X . , X
X . , X . , X .
Here is an example solution:
- - - | | - - -
- - - | | - - -
| | X | | - - -
| | - - - - - -
| | - - - - - -
| | | | | - - -
| | | | | - - -
| | | | | - - -

Cheese Cubes Hint:
no, but why not?

Cheese CubesAnswer:
No. If the grid is checkered so adjacent cubes are different colors,
the mouse must always alternate colors. There are an odd number of
cubes so the mouse must end on the same color as he starts, but the
center is not the same color as the corners.

Measuring with Jugs Hint:
use a series of subtractions.

Measuring with Jugs
Answer:
To measure 4 liters: fill the large jug and pour off 3L by
filling the small jug, to leave 2L. Empty the small jug, and transfer
the 2L over to it. Then fill the large jug again and pour off 1L by
topping off the smaller jug. That leaves 4L in the large jug.
5 - (3 - (5 - 3))
To measure 1 liter: fill the small jug and pour that 3L into the large
jug. Fill the small jug again and pour off 2L by topping off the
large jug. That leaves 1L in the small jug.
3 - (5 - 3)

Burning Fuses Hint:
you can easily add or subtract times, but can you divide by 2?
(Cutting in half doesn't work because they burn unevenly.)

Burning Fuses
Answer:
Light both ends of the 10 minute fuse at once. When those burning
ends meet somewhere in the middle, light the 15 minute fuse. When
that is finished burning, 20 minutes are up. (10/2 + 15)

Rope Escape Hint:
it can be done.

Rope Escape
Answer:
Cut the rope into two pieces of 100 and 50 meters. Tie one end of the
smaller piece to the roof and tie a small loop in the other end around
the middle of the larger piece, so the larger piece is doubled up and
together they hang down 100 meters to the ledge. Climb down to the
ledge and then unthread the 100 meter piece which can be used to climb
down the rest of the way.

Pocket Change Hint:

Pocket Change
Answer:
16 cents: 1 penny, 1 nickel, and 1 dime.

Gloves and Germs Hint:

Gloves and Germs
Answer:
Put both gloves on the same hand and squeeze the 1st culture. Take
the outer glove off and turn it inside out (it is now dirty inside and
clean outside). Use the glove that is still on to squeeze the 2nd
culture. Put the second glove back on over the first (so their dirty
sides touch) and squeeze the 3rd culture.
Each squeeze makes 2 sides of a glove dirty (inside and out). 3
squeezes makes 6 sides dirty, but you only have 4 total sides.
Therefore you know you must somehow re-use the same side that touches
your skin for all 3 squeezes, as above.

Mixed Up Liquids Hint:

Mixed Up Liquids
Answer:
They are equal. Call the initial amount of liquids in the jars J,
measured in teaspoons. When you add a teaspoon of milk to the water,
the milk ratio of the first jar becomes M1 = 1/(J+1) and the water
ratio is W1 = J/(J+1). Then, when you add a teaspoon of the mixture
back to the water, the resulting water ratio is W1/J = 1/(J+1) = M1.

Feynman's Sucking Sprinkler Hint:

Feynman's Sucking Sprinkler
Answer:
The net change in momentum is zero, so it should not spin.
The sucking might tend to make it go backwards, but then the
change in momentum at the corners would cancel that.

Train Full of Water Hint: conserve the center of mass and
conserve momentum and some motion should occur.

Train Full of Water
Answer:
(Subject to debate.) The train moves to the left as the water moves to
the right to get to the spout. But then the water leaving moves to the
left and pushes the train back towards the right to conserve momentum, so
the train ends up with a slight rightward velocity.

Superball Battle Hint:

Superball Battle
Answer:
All the balls return to their shooter, and there are 100 total bounces.
When two bodies of equal mass have an elastic collision in one
dimension, they just swap velocities, as if they pass through each
other. If they did pass through each other, each would pass the 10
balls shot from the other direction, which gives 10x10 total bounces.
Another way: assuming the balls are regularly spaced, bounces occur at
regular time intervals. First 1 bounce, then 2 at once, then 3, etc
up to 10 bounces, and then from 9 back down to 1 again. This sums to
100 total bounces.
Yet another way: the 1st balls bounce 19 times (deflecting the energy
from all the other balls), the 2nd balls bounce 17 times, the 3rd
balls 15 times, etc up to the last balls which bounce only once.
This also sums to 100 total bounces. (There are two of each 1st ball and
2nd ball etc, but each bounce involves 2 balls).

Bubbles in Space Hint:

Bubbles in Space
Answer:
Towards each other.

Flipped Cards Hint:
the two piles could have different numbers of cards and you could flip some cards over (just no looking).

Flipped Cards
Answer:
Take any 10 cards from the deck and flip them all over. Those will
now contain the same number of flipped cards as the rest of the deck.
If x cards of those 10 were already flipped, those will get unflipped,
so both parts now have 10-x cards flipped.

Fox in a Hole Hint:
the fox must alternate between even and odd numbered holes.

Fox in a Hole
Answer:
You can find him in 6 days or less. Search holes 2,3,4 and then
4,3,2. (Other similar patterns also work.) You know the fox must
alternate even and odd holes, so if he got past you on the first
sweep, he can't get by you on the second sweep. Also, you know he
can't hide in the 1st hole on both the 1st and 6th day, or the 5th
hole on both the 3rd and 4h day.

Six Chop Sticks Hint: they are all the same size, and not overlapping.

Six Chop Sticks
Answer:
Make a 3d tetrahedron. Each of its 4 sides is a equilateral triangle.

Stick Boxes Hint: there are 16 total sticks. How does that affect shared sides of 4 boxes?

Stick Boxes
Answer:

If 4 boxes are made from 16 sticks, you know that no boxes can
share edges, only corners.

Fish Sticks Hint:

Fish Sticks
Answer:


Ten Points Hint:

Ten Points
Answer:

Arrange the points in a star shape, with 5 at the star's points, and 5
at the inner intersections.

Connect the Dots Hint:

Connect the Dots
Answer:
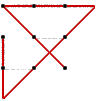
A literal example of "thinking outside the box".

Four Points and Two Distances Hint: a square is one way: the edges are
one distance and the diagonals another. But there are at least 4 other ways.

Four Points and Two Distances
Answer:
There are 6.


Six Marbles Hint: yes you can. How?

Six Marbles
Answer:
Arrange them in the shape of a 3D octahedron, with each pair of colors at opposite vertices.

Wire Cube Hint: think about wire ends and cube corners.

Wire Cube
Answer:
4. Each cube vertex is formed by 3 edges so you need a minimum of one
wire-end for each. There are 8 vertices and 4 wires have 8 ends.

Cube Vision Hint: go with a cube larger than you.

Cube Vision
Answer:
You can see all 6 sides if you are inside a large cube and looking
outwards from near one of the corners.
(For this puzzle you need to think inside the box!)
If you couldn't get inside, then you could instead see 5 sides of a
small cube if you hold it near your nose at a certain angle and look
slightly cross-eyed at it.

Cube Sides Hint: it is less than 6x5x4x3x2 because some of these rotate to equal others.

Cube Sides
Answer:
30
Start with color 1 at the bottom. Any color combination could be
rotated to this orientation, so no different cubes yet. Now for the
top there are 5 possible colors. That leaves 4 colors for the 4
remaining sides, but one of these, say the front, doesn't matter
because we could rotate the other combinations so that color is at the
front. That leaves only 3x2 possibilities for the last 3 sides. So
5x3x2 = 30 all together.
Another way: there are 6! possible color combinations for a given cube
orientation, but this includes 24 copies of each because a cube can be
rotated in 24 different ways. 6!/24 = 30.

Five Triangles Hint: calculate the area and sides of everything first.

Five Triangles
Answer:
The area of each triangle is 1, so the area of the final square will
be 5 and the sides of that square will be
√5
in length. Note that the third side of each triangle is also
√5
so it might make sense to align these on the sides of the square.
Sure enough, this leaves a 1x1 square in the middle which can be
filled by cutting the last triangle into two pieces.


30-60-90 Triangles Hint:

30-60-90 Triangles
Answer: There is one way to make 3, and 4 ways to make 4:
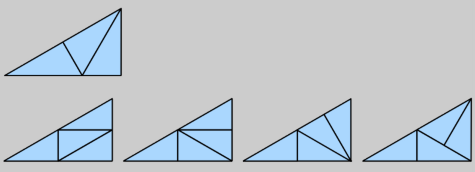
And, there are 64 ways to make 9. If you start with the
configuration below, there are 3 rectangles whose diagonals can each be
flipped to make 2x2x2=8 variations. These changes generate equilateral
triangles whose centers can then each be rotated in 3 ways. The case
above shows how a flipped diagonal makes an equilateral triangle which
is then rotated 3 ways. Three of these 8 variations generate 1
equilateral triangle like above, but three others generate 2 of them
for 3x3=9 combinations, and one generates 3 for 3x3x3=27 combinations.
Adding all these gives 1+3+3+3+9+9+9+27 = 64.


Bookworm Hint:

Bookworm
Answer:
1600 (or maybe 1602 or 1604 if you count the first and/or last pages).
Books are normally arranged on a bookshelf in order starting with
volume 1 on the left, and with their binding facing outwards. Viewing
books this way, the first page of a book is on its right and the last
page is on its left, so the worm actually only eats through the middle
8 volumes.

Five Pirates Hint: what would happen if only 2 pirates were
left playing this game?

Five Pirates
Answer:
The oldest pirate will propose 1 coin for the youngest, 1 for the
middle pirate, and 98 for himself, and 3 of the 5 pirates will approve that plan.
Name the pirates A,B,C,D,E from youngest to oldest, and work back from
2 pirates, assuming the others had been thrown overboard because their
plan did not pass:
If 2 pirates: B proposes "0, 100" for A and B giving all coins to himself because his 50% vote is enough to pass any plan.
If 3 pirates: C proposes "1, 0, 99" (for A,B,C) and A would approve because otherwise he'd get nothing on the next round with 2 pirates above.
If 4 pirates: D proposes "0, 1, 0, 99" (for A,B,C,D) and B would approve because otherwise he'd get nothing on the next round.
If 5 pirates: E proposes "1, 0, 1, 0, 98" and A and C approve because otherwise they'd get nothing on the next round.
The pirates are intelligent enough to anticipate all of this, and so
only the last case actually occurs, with nobody being thrown
overboard.
Of course if they were very intelligent they wouldn't have agreed to
these rules in the first place...

100 Pirates Hint:

100 Pirates
Answer:
The oldest 26 pirates will be thrown overboard. The 74th oldest will
then propose giving one coin to 5 of the youngest 42 pirates, and this
will be approved by 50% of the vote.
Number the pirates from youngest to oldest, and work back from 2
pirates, assuming the others had been thrown overboard because their
plan did not pass. This starts out similar to the 5 pirate version
of this puzzle, but then gets more interesting:
If 2 pirates: #2 proposes "0, 5" giving all coins to himself because his 50% vote is enough to pass any plan.
If 3 pirates: #3 proposes "1, 0, 4"
If 4 pirates: #4 proposes "0, 1, 0, 4"
If 5 pirates: #5 proposes "1, 0, 1, 0, 3"
If 6 pirates: #6 proposes "0, 1, 0, 1, 0, 3"
If 7 pirates: #7 proposes "1, 0, 1, 0, 1, 0, 2"
If 8 pirates: #8 proposes "0, 1, 0, 1, 0, 1, 0, 2"
If 9 pirates: #9 proposes "1, 0, 1, 0, 1, 0, 1, 0, 1"
If 10 pirates: #10 proposes "0, 1, 0, 1, 0, 1, 0, 1, 0, 1"
If 11 pirates: #11 proposes "1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 0" These can't keep any for themselves, but they live.
If 12 pirates: #12 proposes "0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 0"
If 13 pirates: #13 would get thrown overboard because the 7 of the first 12 not offered a coin will vote against him.
If 14 pirates: #14 proposes "1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 0*, 0, 0, 0" and the 5 offered coins plus #13 and #14 approve this.
If 15 to 17 pirates: these all get thrown overboard because the 9 of the first 14 not offered a coin will vote against them.
If 18 pirates: #18 proposes "0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 0, 0, ..." and the 5 offered coins plus #15 to #18 approve this.
If 19 to 25 pirates: these all get thrown overboard because the 13 of the first 18 not offered a coin will vote against them.
If 26 pirates: #26 proposes "1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 0, 0, 0, ..." and the 5 offered coins plus #19 to #26 approve this.
If 27 to 41 pirates: these all get thrown overboard because the 21 of the first 26 not offered a coin will vote against them.
If 42 pirates: #42 proposes "0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 0, 0, ..." and the 5 offered coins plus #27 to #42 approve this.
If 43 to 73 pirates: these all get thrown overboard because the 37 of the first 42 not offered a coin will vote against them.
If 74 pirates: #74 proposes "1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 0, 0, 0, ..." and the 5 offered coins plus #43 to #74 approve this.
If 75 to 100 pirates: these all get thrown overboard because the 69 of the first 74 not offered a coin will vote against them.
*Note that for 14 pirates above, the proposal could actually include 1
coin for any 5 odd numbered pirates from the first 12. Then
for 18 pirates, the proposal could include 1 coin for any 5 of the
first 14 pirates, even or odd, because those offered a coin should
approve since they are not 100% certain to get one in the round with 14
pirates. The same is true for 26, 42, or 74 pirates.

Five Hats Hint:

Five Hats
Answer:
Assume they are looking right in the order A,B,C. If A saw two black
hats he would know he had white. If B saw one black and A didn't say
anything, he would know he had white. But neither A nor B say
anything because they only see white hats, so then C knows he must have white.

Pop Quiz Hint:

Pop Quiz
Answer:
This inductive reasoning leads you to claim the surprise can't be on any
day, and therefore doesn't actually differentiate any of them.

Darts Hint:

Darts
Answer:
2/3. This is just another way of saying: what are the chances
that your third dart is not the best.

Girl Babies Hint:

Girl Babies
Answer:
The male to female ratio is 50/50. The odds of each new baby are
always 50/50, and a rule for when families stop having children does
not affect those odds.
The population size also stays the same, because there are 2 children
per family on the average. They all have 1 girl, and the boy/girl
ratio is 50/50 so they must also have an average of 1 boy.
Another way to calculate this is as follows: All families have 1 girl.
Prior to that, 1/2 of the families also have at least one boy, 1/4
have another boy, 1/8 have another, etc. The sum of the series (1/2 +
1/4 + 1/8 + 1/16...) equals 1. So on the average its just 1 girl and
1 boy.

Hotel Bellboy Hint:

Hotel Bellboy
Answer:
You wouldn't add the bellboys $2 to the $27, you would subtract it.
They paid $27, the bellboy kept $2, and $25 was for the room.

Doctor Who Hint:

Doctor Who
Answer:
The doctor is his mother. (Shame on you if you didn't think of that.)

Two Fathers and Two Sons Hint:

Two Fathers and Two Sons
Answer:
There was a grandfather, father, and son. The father counts as both a father and a son.

Two Boys and a Boat Hint: there are two ways to cross a river.

Two Boys and a Boat
Answer:
The boys start on opposite sides of the river.

4 People and a Bridge Hint: it can be done in less than 21 minutes.

4 People and a Bridge
Answer:
17 minutes.
1 crosses with 2, 1 returns with the torch, 7 crosses with
10, 2 returns with the torch, and crosses back with 1. (2 + 1 + 10 + 2 + 2)

Defying Death Hint:

Defying Death
Answer:
He said: "I will be fed to lions."

Non-Self Containing Sets Hint:

Non-Self Containing Sets
Answer:
If this superset (of all sets that don't contain themselves) contains
itself, then it shouldn't, and vice versa.

Manhole Covers Hint:

Manhole Covers
Answer:
So they don't fall in. A square cover nearly the same size and shape
as the hole, for example, could fit into the hole diagonally.

Mirrors Hint:

Mirrors
Answer:
Mirrors actually flip things front-back. Flipping left-right and then
rotating about a vertical axis gives the same transform. A "mirror
image" is more easily perceived this way, probably because humans are
left-right symmetrical. You could also think of this transform as
flipping up-down and then rotating about a horizontal axis but this is
harder to visualize unless you turn your face sideways first.

Mind Reading Trick
Answer:
Elephant!
You are first computing 10x - x = 9x. The digits of small multiples
of 9 always sum to 9 so after subtracting 4 you always get 5 and E no
matter what number you picked at first. Most people will then
select elephant because there aren't many other common land animals
that start with E, although somebody might pick Emu or Elk.

Centrifuge Hint:

Centrifuge
Answer:
Yes. You can independently balance 3, and then 2. Put 3 in equally
spaced from each other, such as in slots 1, 5, and 9. Then put in the
other 2 opposite each other, such as in slots 2 and 8.

1000 Doors Hint:

1000 Doors
Answer:
The doors whose number equals a perfect square are open. Those with
an odd number of factors, including 1 and the number, are open, and
only perfect squares have an odd number of factors.

Three dice Hint:

Three dice
Answer:
1/8. All 3 must be odd for the product to be odd. 1/2 x 1/2 x 1/2 = 1/8

Two Dice at 7 Hint:

Two Dice at 7
Answer:
1/6. There are 6x6=36 possible combinations and 6 of those give 7
(1+6, 2+5, 3+4, 4+3, 5+2, 6+1). Another way to think of it is for any
number on the 1st dice, there is always one number on the 2nd dice
that will give 7 so no matter what you roll first, you still have a
1/6 chance of getting 7 total.

Four Dice at 14 Hint:

Four Dice at 14
Answer:
146/1296 = 11.265%
This problem can be tedious to solve, but here is a way that isn't too
bad. There are 6x6x6x6 = 1296 possible combinations for 4 dice, and
we want to find how many of those will sum to 14. No matter what you
roll for the 1st two dice, you can still get 14 in the end, so we can
go through the possible results of the 1st two dice (2 to 12) and ask
how many ways are there to get to 14 for each of those.
For the 2+12 case: there is only 1 way the 1st two dice can give 2
(1+1), and only 1 way the 2nd two dice can give 12 (6+6) so there is
just 1 combination there.
For the 3+11 case: there are 2 ways the 1st two dice can give 3
(1+2 or 2+1) and for each of those there are 2 ways the 2nd two dice
can give 11 (6+5 or 6+5), so 2x2 combinations there.
For the 4+10 case: there are 3 ways the 1st two dice can give 4
(1+3, 2+2, 3+1), and 3 ways the 2nd two dice can give 10 (4+6, 5+5
6+4), so 3x3 combinations there.
For the 5+9 case: there are 4 ways the 1st two dice can give 5,
and 4 ways the 2nd two dice can give 9, so 4x4 combinations there.
And so on for the 6+8, 7+7, 8+6, 9+5, 10+4, 11+3, and 12+2 cases.
When we add all these together we get 1x1 + 2x2 + 3x3 + 4x4 + 5x5 +
6x6 + 5x5 + 4x4 + 3x3 + 2x2 + 1x1 = 146 total ways to get 14 out of
the 1296 total combinations.
Note that your chances of getting a 4 instead are just 1/1296 or
146 times less likely than getting a 14.

Meet in the Middle Hint:

Meet in the Middle
Answer:
2/3 of the original asking price. You are offering: 1/2 + 1/8 +
1/32... and the salesman is reducing his price by 1/4 + 1/16 + 1/64...
At each step the price is reduced by half the amount that your offer
increased, so the final price should also be twice the amount of the
final discount. (1/2 + 1/8 + 1/32...) = 2 x (1/4 + 1/16 + 1/64...)
These have to sum to 1 so the final price is 2/3 (with a discount of
1/3).
Thanks to Arlo Sims for proposing this puzzle and its solution.

Alien Hats Hint: there is a way!

Alien Hats
Answer:
The first person can say "white" if they see an odd number of white
hats in front of them or "black" for an even number. The 2nd person
can then calculate the correct color of their hat: if the number of
white hats they see has a different odd/even result, then theirs must
be white. The others can each in turn adjust the original odd/even
result based on what all the people behind them say (each "white"
answer flips it) and then compare that to the number of white hats
they see to figure out the correct color of their hat. Planet saved.

100 Prisoners and 100 Boxes Hint: there is actually a way that
saves them more than 1/4 of the time, but this is a hard puzzle, good
luck!

100 Prisoners and 100 Boxes
Answer:
Number the prisoners 1 to 100. Each prisoner uses the following
rule: First inspect the box matching your number. Then convert the
prisoner's name found in that box to his number and inspect that box
next. Repeat until you either find your own name or use up your 50
tries.
Amazingly this allows all of them to find their own names slightly
more than 30% of the time! This consistent box searching order
creates loops where a given name is certain to be within the loop of
boxes being searched. If no loops happen to contain more than 50
boxes, all of them will succeed.

Wire Ends Hint: try twisting some wires together and then take
both the battery and light bulb with you.

Wire Ends
Answer: It is possible.
Here is one way: first on the mainland, leave 2 wires unconnected, and
twist the others together in pairs (blue). Bring both the battery and
light bulb with you to the island, and test the connectivity between
wires there to identify the pairs and unconnected wires on that end.
Then twist these ends together in different pairs (red) to form a
"chain" pattern with the previous pairs, but leave the last 2
unconnected. Label these 1 to 36. Return to the mainland and,
remembering their initial groups, determine the new pairings. The
previously unconnected wire that is now connected is #1, and its new
pair is #2. The previous pair of that is #3, and the new pair of that
is #4, etc. Work your way through the chain, and the final
unconnected wire is #36.
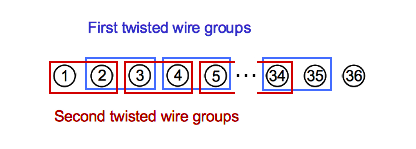
This method should work for any number of wires, but for an odd number
leave a single wire unconnected instead of two.
Another way:
first on the mainland, twist 8 groups of wires together with each
group having a different number of wires, from 1 to 8. Bring both the
battery and light bulb with you to the island and test the
connectivity between wires to identify each of these groups on that
end. Then, remembering their initial groups, twist the ends together
again with 1 to 8 wires per group, but differently such that every
wire in the same initial group is now in a different group. Number
the wires uniquely based on their first and second groups. Then
return to the mainland and, remembering their initial groups, test
connectivity to determine the second group and finally label those
ends to match.

Note that this second method only works if the number of wires is a
"triangular" number, which is the sum of 1 to N
integers. (1+2+3+4+5+6+7+8 = 36)

Ball Paths Hint:
how many ways can the ball get to the boxes in the 2nd and 3rd row?

Ball Paths
Answer:
70. The number of possible paths to any given box is the sum of the
possible paths to each of the two boxes above it. There is only 1
possible path for each box on the top edges (all lefts, or all rights)
and filling in numbers for each other box by summing its two neighbors
above, gives 70 total possible paths for the bottom box.

Some of you may recognize this as Pascal's triangle of binomial
coefficients, but with the bottom corners missing.

Ball Paths 2 Hint: how many left vs right
options did each have?

Ball Paths 2
Answer:
The red path is more likely. It has 1/16 chances because there are 4
forks along the way, each with 1/2 chances of happening. 1/2 x 1/2 x
1/2 x 1/2 = 1/16. Once the ball gets to a box on the bottom left edge
it has no option but to fall right towards the center. The green path
has only 1/128 chances of happening because it has 7 forks along the
way, each with 1/2 chances. The green path may look more "random" but
that exact path is much less likely because the ball has more options
when it stays away from the bottom edges.

Square of Bugs Hint:

Square of Bugs
Answer:
1 meter. A bug's movement remains perpendicular to the next bug's, so
the total distance is the same as if the bug being chased was
stationary. They start out 1 meter apart so that is the total
distance traveled when they meet in the center.
Another solution method: They must meet in the center, and the
distance from a corner to the center is
1/√2.
The bugs always head at 45 degrees relative to the center, so they
will travel a total of √2
times that distance.
1/√2 x √2 = 1

Bike Speed Hint:
It is not 4 minutes as you might think.

Bike Speed
Answer:
1 mile in 3.75 minutes
His speed with no wind should be the average of his speed with the
wind and his speed against the wind. His speeds are 1/3 and 1/5
miles per minute respectively, and the average of these is 4/15
miles per minute. This corresponds to 1 mile in 15/4 minutes or 3.75 minutes.

A Bee and Two Trains Hint: there is an easy way
and a hard way to solve this one.

A Bee and Two Trains
Answer:
50 miles. The trains travel for 2 hours until they meet, and the bee
flies at 25 mph the whole time, so he flies 50 miles. (Hope you didn't
try to calculate each zig and zag!)

Backwards Bee and Two Trains Hint: trick question.

Backwards Bee and Two Trains
Answer:
There is no way to know. Trick question.

Water Levels Hint: think about volume and weight
and displacement in each case.

Water Levels
Answer:
The stone sinks and then displaces less water than when it was being
floated by the boat, so the water level falls.
The log floats and continues to displace the same amount of water as
its weight, so the water level stays the same.

Refueling Hint: without refueling, a ship can only fly 1/4
of the way around the planet before it needs to head back to port. So
you'll need to use both refueling ships multiple times.

Refueling
Answer:
First fill all 3 tanks and fly the 3 ships together 1/8 of the way
around the planet, using 1/4 of each tank. Then one refueling ship
transfers 1/4 tank to each of the other 2 ships to refill both,
leaving itself 1/4 tank to return to port. The remaining two ships
use another 1/4 of their tanks to reach 1/4 of the way around the
planet. Then the 2nd refueling ship fills your ship back up by giving
you another 1/4 tank, leaving itself 1/2 tank to return to port. Now
your ship has enough fuel to fly from 1/4 all the way to 3/4 around
the planet. Meanwhile the first ship refills at the port, and flys
the other way to meet you at the 3/4 point where it gives you half its
remaining fuel, allowing both ships to make it to 7/8 around. The 2nd
refueling ship refills and meets you both there to give you each a
final 1/4 tank so you can all return safely to port.

Pieces of Stone Hint: he can put pieces on
either side of the scale.

Pieces of Stone
Answer:
1, 3, 9, and 27. You can put multiple pieces on the scale to add
their weights, or put pieces on the other side to subtract them.

Breaking Balls Hint: once one ball breaks, you'll need to test
the remaining floors one by one from the ground up with that many
possible drops. How many floors can you safely test with only 3
drops?

Breaking Balls
Answer:
You can do it in 14 drops. You can't use a normal divide-by-2 search
here because once the first ball breaks you'll need to search all the
untested floors below from bottom to top. To find the best strategy,
work backwards from fewer floors:
1 drop allows you to test 1 floor.
2 drops can test 3 floors: Test the 2nd floor first. It it breaks,
test the bottom floor with the other ball. If not, test the top floor
with either ball.
3 drops can test 6 floors: Test the 3rd floor first. If it breaks
test the bottom 2 floors in order with the other ball. If not, test
the top 3 floors as described above.
4 drops can test 10 floors: Test the 4th floor first. If it breaks
test the bottom 3 floors in order with the other ball. If not, test
the top 6 floors as described above.
N drops allows you to test the number of floors equal to the sum of 1
to N. 14 drops can test 105 floors: Test the 14th floor first. If it
breaks test the bottom 13 floors in order with the other ball. If
not, test the 27th floor next (14+13), and so on.
For any given drop, the number of drops you'll need after that should
be the same if that ball breaks or not (or sometimes they are off by 1
if your total is not an even sum-of-1-to-N).

Puzzling Scales Hint: You can solve this with algebra (1 top +
3 blocks = 12, etc.) or you can first just figure out how many marbles a
block weighs by looking at the first two scales.

Puzzling Scales
Answer:
9 marbles
Substitution method: the middle scale shows 1 top = 1 block + 8
marbles. Exchanging the top from the first scale with those you get 4
blocks + 8 marbles = 12 marbles. You can remove 8 marbles from each
side of that so 4 blocks balance 4 marbles and a block must weigh the
same as a marble. Now from the middle scale you also know the top
weighs 9 marbles.
Subtraction method: subtract the contents of both sides of the middle
scale from the same sides of the first scale to get: 3 blocks = 4
marbles - 1 block. Subtracting a block on the right is the same as
adding it to the left (add a block to both sides) so 4 blocks = 4
marbles, and so the top weighs 9 marbles.
Another variation: Take the middle scale and add 3 blocks to each side. Now
its left side is equal to the first scale's left side, so the right
sides must also be equal. Since 4 blocks + 8 marbles = 12 marbles, a
block must weight the same as a marble, and so the top weighs 9 marbles.

Magic Microbes Hint: No single microbe appears or splits in two. It is a group effort.

Magic Microbes
Answer:
Notice that the top of microbe #7 shifts to a position "*" where there
was no microbe before, only a bubble. Then the top of #7 is replaced
by #1, which is replaced by #10, and so on... except at the end of the
chain, the top of #6 is only replaced by the top of a bubble.

If we change the order of the original 14 microbes so the tops all
just shift to the left, instead of swapping back and forth, you can
see how an extra is created when all the tops shift relative to the
bottoms. However no single microbe can really be considered the new
one. The area of each new microbe decreases slightly on the average
to make 15 total instead of 14. The nuclei undergo a similar effect.
The 4 nuclei crossing the center line (8,2,11,5) create 5 slightly
smaller nuclei when they shift over.
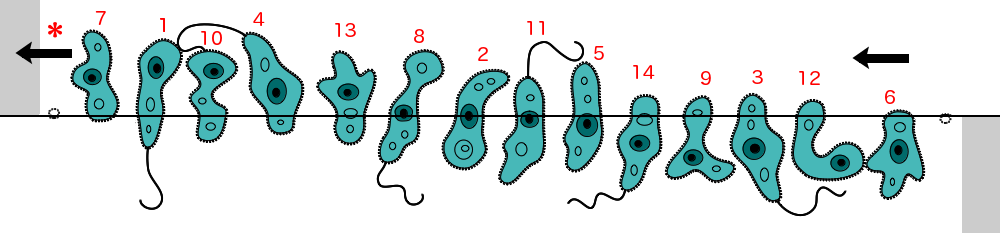


Handshakes Hint: There are 10 people and nobody shakes their
own hand or their partner's, so the maximum number must be 8. What can
you know about the partner of the person who shook 8 hands?

Handshakes
Answer:
Jack and his wife both shook 4 hands.
The 9 different answers must be 0 through 8 since there are 10 people
and nobody shakes their own hand or their partner's.
Whoever shook 8 hands, shook all the others except their partner's,
which means all those others shook at least once, so the partner of
the person who shook 8 hands must be the one who shook 0 hands.
Whoever shook 7 hands, shook all the others except their partner's and
the person who shook 0 hands, which means those others shook at least
twice, so the partner of the person who shook 7 hands must be the one
who shook 1 hand.
Whoever shook 6 hands, shook all the others except their partner's and
the people who shook 0 or 1 hands, which means those others shook at
least 3 hands, so the partner of the person who shook 6 hands must be
the one who shook 2 hands.
Whoever shook 5 hands, shook all the others except their partner's and
the people who shook 0, 1, or 2 hands, which means those shook at
least 4 hands, so the partner of the person who shook 5 hands must be
the one who shook 3 hands.
The remaining two people each shook 4 hands, because they shook with
the 5,6,7 and 8, but not with the 0,1,2 or 3. And this couple has to
be Jack and his wife, because his wife is the last one left in the 9
different answers. Jack can have the same number of shakes because he
didn't ask himself and isn't one of the 9. So Jack and his wife both
shook 4 hands.


Three-Way Dual Hint: having bad aim might be good for Joe.

Three-Way Dual
Answer:
For his first shot, Joe should shoot at the ground, and he is the most likely to
survive.
In this case John will then shoot at Jack, and if he misses,
Jack will shoot back at John and hit him. (They will each shoot at
the man who is the better shot, which is not Joe.) Then Joe can shoot
at whoever is still standing, giving him a little more than 50/50
chances of surviving (about 55.4% because if he shoots at John and
misses, John could miss shooting back, extending to further rounds).
If Joe instead first shot at Jack and hit him, then John would shoot
at Joe and get him 3/4 of the time, so Joe actually has better chances of
surviving if he doesn't shoot at anybody on the first round.

Find the Cable Hint: you could dig along any 3 sides for 3 km
total, or dig a big X connecting the 4 corners for 2.828 km, but the
best solution is below 2.7 km.

Find the Cable
Answer:
2.639 km.
You know each corner of the square must be included in the pattern of
ditches because the cable could just barely pass under any corner.
Here are 6 different solutions, each one an improvement on the previous.
1. Dig around the entire perimeter of the square for 4 km total.
2. Dig just along any 3 sides of the square for 3 km total. You could
also dig 2 opposite sides with a perpendicular line connecting them
like an "H" or "I" shape which also gives 3 km total.
3. Dig along both diagonals in an "X" shape for
2√2
= 2.828 km total.
4. The minimal path connecting the 4 corner points has 120°
angles between segments, like connected soap bubbles or veins
in a leaf. The total this way is
1 + √3 = 2.732 km.

5. However, you can beat that with two sides and half a diagonal that are not all connected.
This gives
2 + √2/2
= 2.707 km.
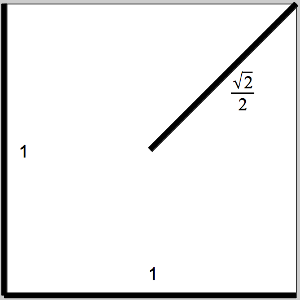
6. But wait, now if you apply the minimal-path trick using 120° connections to those 3 corners, you get this:

They connect at [x,x] where (1-x)/x = tan(120° - 45°) and x = 1/(3 + √3)
Using this pattern, the total is
√2/2 + 2√2/√3 + √2/(3 + √3)
which simplifies to
√2 + √6/2 = 2.639 km.



















