Make the Platonic Solids with Lights Karl Sims Here are instructions for creating large versions of these classic 3D shapes with strings of LED lights. A Platonic solid is a regular convex polyhedron with a single type of regular polygon for its faces. Each vertex is also similar and joins an equal number of edges. These are named after the Greek philosopher Plato. Only five such shapes exist.

	Tetrahedron	Cube	Octahedron	Dodecahedron	Icosahedron
	4 triangles 4 vertices 6 edges	6 squares 8 vertices 12 edges	8 triangles 6 vertices 12 edges	12 pentagons 20 vertices 30 edges	20 triangles 12 vertices 30 edges

These polyhedra are constructed using wooden poles for spokes that connect each vertex to a small cube at the center, and lights are strung between the spokes along each edge. "Fairy lights" have LEDs that align nicely along their wire and are visible from all sides. They are available in strings of various lengths, and seem to consistently have a 4" distance between LEDs, so we'll use edge lengths of even multiples of 4" to get an equal number of lights per edge. The specific spoke lengths and number of lights required will depend on the sizes you choose to make each shape below.

Materials:

• 5 strings of LED "fairy lights" of various lengths, with power adapters
• 50 wooden dowels 1/4" diameter, of various lengths for the spokes
• 5 small wooden cubes, about 1¾"
• misc other wood for support jigs
• paint, if desired

Tools:

• Drill press
• Band saw, jig saw, or fine hand saw
• Soldering iron
• Wire cutters or scissors
• Pliers
• Measuring tape
• Sand paper

Drill holes in the cubes

The spokes of each Platonic solid can conveniently be attached to the corners and/or faces of a cube at its center.

	Tetrahedron 4 spokes	Cube 8 spokes	Octahedron 6 spokes	Dodecahedron 20 spokes	Icosahedron 12 spokes

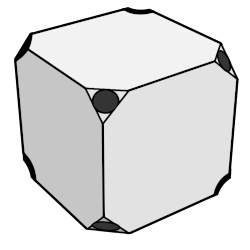
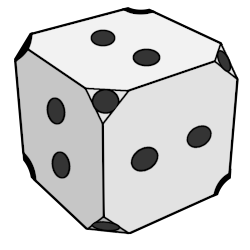
Drill a 1/4" hole for each spoke into the 5 cubes using the patterns shown. If your dowel is too tight in a 1/4" hole try a 17/64" drill bit instead. Drill to a depth of about 1/4" from the center of the cube.

It will help to create a simple jig to support a cube while drilling a hole into its corner straight along its 3D diagonal. Clamp a board to your drill press and drill a ½" hole in it. Rest a corner of the cube in that hole and align the opposite top corner with a smaller drill bit so the cube's diagonal is precisely vertical. Then glue 3 small blocks to the board pushed against the lower faces of the cube to hold it steady at that angle.

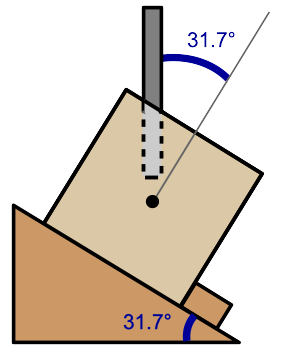
The center cube for the dodecahedron also requires two holes drilled into each face at a 20.9° angle, and for the icosahedron at a 31.7° angle. Tilt your drill press platform or create two small ramp jigs to hold the cube at these angles when drilled. Position each hole so it is aimed towards the center of the cube, and turn the cube 180° to drill the second hole on the same face. Align the pairs of holes on each face in alternating directions as shown above.

	For the dodecahedron		For the icosahedron

Make the spokes

Saw a ¼" notch into one end of each wooden dowel to support the strings of lights. Select a size for each polyhedron in the tables below, and cut the dowels to the corresponding spoke length for each. Note that the spoke lengths may need to be adjusted slightly based on the actual depth of the holes in the cube, and the actual depth of the notches in the spokes. Insert a spoke and check the distance between the notch and the cube center, or to the opposite notch. Adjust the spoke lengths carefully so your light strings will not be too tight or too loose. Insert the spokes into the cubes, and paint if desired. The examples shown below were painted with flat black spray paint.

Attach the lights

Wrap the lights between the ends of the spokes. Secure the wire to the first spoke with some hitches, and align the lights equally on each edge. If you put one light right next to the spoke, each vertex should end up with multiple lights as the examples show.

To reach all the edges of a polyhedron with a single string of lights, you'll need to wrap the lights twice along some of the edges. The LEDs on one of the double wires can be individually disabled by pinching them with pliers, so all the edges still have an equal number of active lights. It should be easy to find a path that uses the minimum number of doubled edges for the tetrahedron, cube, and octahedron, but here are suggested paths for wrapping the lights on the dodecahedron and icosahedron:

After snipping off the extra lights at the end of the string, you may need to reconnect two of the wire strands, if your wire is 3-stranded. Use a piece of metal to test which two ends need connecting and solder them together.

Secure the end of the wire to the last spoke.

Notes on the values in these tables:
Edge length:	assumes 4" between lights.
Total lights:	Lights per edge × (Edges + Edges needing double lights) + 3 extra lights for sufficient wire at the ends.
Total width:	predicts the smallest doorway the structure could fit through once assembled.
Spoke length:	the center-to-vertex radius of the polyhedron.

Tetrahedron

Spokes:   4 Edges: 6 Edges needing double lights:   1 Total width / Edge length: 0.707 Spoke length / Edge length: 0.612 Lights per edge:    9 10 11 12 13 Edge length: 36" 40" 44" 48" 52" Total lights: 66 73 80 87 94 Total width: 25.46" 28.28" 31.11" 33.94" 36.77" Spoke length: 22.05" 24.49" 26.94" 29.39" 31.84"

Cube

Spokes:   8 Edges: 12 Edges needing double lights:   3 Total width / Edge length: 1 Spoke length / Edge length: 0.866 Lights per edge:    5 6 7 8 9 Edge length: 20" 24" 28" 32" 36" Total lights: 78 93 108 123 138 Total width: 20" 24" 28" 32" 36" Spoke length: 17.32" 20.78" 24.25" 27.71" 31.18"

Octahedron

Spokes:   6 Edges: 12 Edges needing double lights:   0 Total width / Edge length: 0.816 Spoke length / Edge length: 0.707 Lights per edge:    6 7 8 9 10 Edge length: 24" 28" 32" 36" 40" Total lights: 75 87 99 111 123 Total width: 19.60" 22.86" 26.13" 29.39" 32.66" Spoke length: 16.97" 19.80" 22.63" 25.46" 28.28"

Dodecahedron

Spokes:   20 Edges: 30 Edges needing double lights:   9 Total width / Edge length: 2.23 Spoke length / Edge length: 1.40 Lights per edge:    2 3 4 5 6 Edge length: 8" 12" 16" 20" 24" Total lights: 81 120 159 198 237 Total width: 17.82" 26.72" 35.63" 44.54" 53.45" Spoke length: 11.21" 16.82" 22.42" 28.03" 33.63"

Icosahedron

Spokes:   12 Edges: 30 Edges needing double lights:   5 Total width / Edge length: 1.51 Spoke length / Edge length: 0.951 Lights per edge:    4 5 6 7 8 Edge length: 16" 20" 24" 28" 32" Total lights: 143 178 213 248 283 Total width: 24.18" 30.23" 36.28" 42.32" 48.37" Spoke length: 15.22" 19.02" 22.83" 26.63" 30.43"

The cubeoctahedron requires holes drilled diagonally into each of the 12 edges of the center cube. Its Total width / Edge length ratio is 1.41, and its Spoke length is exactly equal to its Edge length.

The rhombic dodecahedron requires holes in each face and corner of the center cube, like for the octahedron and cube combined. Its Total width / Edge length ratio is 1.73, and it has two different spoke lengths: 6 with a Spoke length / Edge length ratio of 1.15, and 8 spokes with a length exactly equal to the Edge length.

The stellated octahedron also requires holes in each face and corner of the center cube. Its Total width / Edge length ratio is 1.41, and it also has two different spoke lengths: 6 with a Spoke length / Edge length ratio of .707, and 8 spokes with a Spoke length / Edge length ratio of 1.22. This shape can be simplified by omitting the interior octahedral edges and using just 8 spokes to make two intersecting tetrahedra.

The truncated octahedron requires 4 holes in each face of the center cube at a 26.6° angle, like for the icosahedron but with holes near all 4 edges of each face in a diamond pattern. Its Total width / Edge length ratio is 2.45, and its Spoke length / Edge length ratio is 1.58.

Further reading:
Wooden Book by Daud Sutton: Platonic & Archimedean Solids
Wikipedia pages for: Dual polyhedra, Archimedean solids, Catalan solids, stellated polyhedra, compound polyhedra, and 4 dimensional polytopes.

Back to other work by Karl Sims